آزمون مربع کای يا خی دو

خی دو یا آزمون مقایسه داده های مستقل رده اي

به منظور بررسی ارتباط بین دو متغیر مستقل رده ای، چنانچه متغیرهای مورد نظر بیش از دو رده داشته باشند، داده های آن ها را در یک جدول r*c خلاصه می کنیم. که در آن r تعداد رده های متغیر سطری و c تعداد رده های متغیر ستونی است:

فرض صفر مورد آزمون، استقلال متغیرهای سطری و ستونی و یا به عبارت دیگر یکسان بودن نسبت یکی از رده های متغیر سطری در رده های دیگر متغیر ستونی (یا برعکس) می باشد، که آن را به صورت H_0: p_i1=p_i2=⋯=p_ic با یک رده معین i از متغیر سطری نشان می دهند، (i=1,2,…,r).

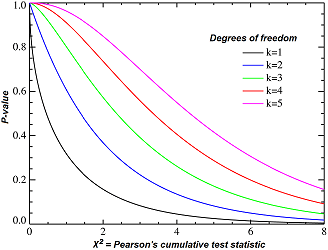
در صورت بزرگ بودن حجم نمونه از آماره آزمون از توزیع مجانبی مربع کای پیروی می کند. آماره آزمون به صورت زیر تعریف می شود :

که در آن O_ij فراوانی مشاهده شده در خانه ij جدول و E_ij مقدار مورد انتظار خانه ij تحت فرض H_0 می باشد. یعنی :

، درجه آزادی آماره مورد آزمون برابر (r-1)(c-1) است. شرط برقراری تقریب آن است که در تمامی خانه های جدول : E_ij≥5 .

جهت دانلود پکیج آموزشی آزمون کای دو در اس پی اس اس (chi-square) کلیک کنید.

ضریب فی (φ) معیاری از ارتباط است که برای ارزیابی رابطه بین دو متغیر طبقه‌بندی، هر کدام دارای دو سطح (متغیرهای باینری) استفاده می‌شود. این ضریب مشابه ضریب همبستگی پیرسون است، اما به طور خاص برای داده های اسمی (مقوله ای) طراحی شده است.

ضریب فی از -1 تا +1 متغیر است:

1+ نشان دهنده یک ارتباط مثبت کامل است: هر دو متغیر تمایل دارند با هم رخ دهند.
0 نشان دهنده عدم ارتباط است: هیچ الگوی ثابتی بین متغیرها وجود ندارد.
-1 یک ارتباط منفی کامل را نشان می دهد: وقتی یک متغیر رخ می دهد، دیگری تمایل دارد رخ ندهد.

فرمول محاسبه ضریب فی از جدول احتمالی (جدول 2×2) به شرح زیر است:

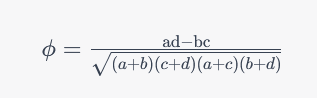
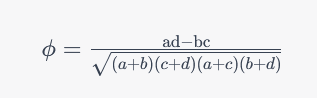
جایی که:

“a” نشان دهنده فراوانی سطح اول متغیر اول و سطح اول متغیر دوم است.
“b” نشان دهنده فراوانی سطح اول متغیر اول و سطح دوم متغیر دوم است.
“c” نشان دهنده فراوانی سطح دوم متغیر اول و سطح اول متغیر دوم است.
“d” نشان دهنده فراوانی سطح دوم متغیر اول و سطح دوم متغیر دوم است.

یادت باشه:

ضریب فی برای متغیرهای دسته بندی باینری مناسب است.
مانند سایر ضرایب همبستگی، Phi فقط قدرت ارتباط را ارزیابی می کند، نه علیت.
Phi به توزیع فرکانس ها، به خصوص در نمونه های کوچک حساس است.

برای تفسیر ضریب فی:

اگر φ نزدیک به +1 یا -1 باشد، ارتباط قوی بین متغیرها وجود دارد.
اگر φ نزدیک به 0 باشد، هیچ ارتباطی وجود ندارد.

شما می توانید از نرم افزارهای آماری مانند R، Python (با کتابخانه هایی مانند SciPy یا StatsModels)، یا بسته های آماری اختصاصی برای محاسبه ضریب Phi و انجام تست های معناداری استفاده کنید.

مثالی از آزمون خی دو (مربع کای)

فرض کنید که تولید یک محصول در سه نوبت کاری مختلف صورت می گیرد. عیوب ممکن محصول از 4 نوع متفاوت است. تعداد عیب های مشاهده شده در 3 نوبت کاری در قالب جدول زیر نشان داده شده است:

آیا نوبت کاری و نوع غیب مشاهده شده از یکدیگر مستقل هستند؟

در واقع فرض آزمون است که در آن نوع عیب i ام می باشد.

برای حل مسئله ابتدا مقادیر مورد انتظار را تحت فرض یکسانی انواع عیب ها در نوبت های کاری مختلف محاسبه می کنیم.

سپس با استفاده از رابطه (1) مقدار آماره محاسبه می شود که برابر 19.17 بدست می آید.

این مقدار با عدد حاصل از جدول توزیع کای دو با 6= 2*3=(r-1)(c-1) در سطح خطای آلفا مقایسه می شود. این عدد برابر 12.592 می باشد.

بنابراین از آنجایی که 12.592< 19.17 است، نوبت کاری و نوع عیب مشاهده شده، مستقل هستند. به عبارت دیگر بروز انواع عیب ها تحت تأثیر نوبت های کاری قرار ندارد.

منبع : مقدمه ای بر روش های آماری ناپارامتری / نوشته : اکبر گلدسته / انتشارات جهاد دانشگاهی / 1390

جهت دانلود پکیج آموزشی آزمون کای دو در اس پی اس اس (chi-square) کلیک کنید.

مقالعه ای که در بالا آن را مطالعه فرمودید مربوط به بحث آزمون مربع کای يا خي دو است ،که تیم تحلیلی یونی تحلیل آن را برای شما عزیزان و پژوهشگران گرد آوری کرده است.

آزمون مربع کای يا خی دو