آمار پارامتری و روش‌های تجزیه و تحلیل مرتبط

موضوع نوشته : آمار پارامتری و روش‌های تجزیه و تحلیل مرتبط

آمار پارامتری

در حوزه «تجزیه و تحلیل آماری داده‌ها» (Statistical Data Analysis)، توزیع جامعه آماری که نمونه از آن گرفته شده، مهم است زیرا هر چه اطلاعات بیشتر در زمینه رفتار داده‌ها و شکل پراکندگی و توزیع آن‌ها وجود داشته باشد، نتایج قابل اعتمادتر و دقیق‌تر خواهند بود. در مقابل، وجود اطلاعات کم از توزیع جامعه آماری مربوط به نمونه، باعث کاهش اعتماد به نتایج حاصل از روش‌های معمول (پارامتری) آماری می‌شود. بنابراین در این حالت مجبور به استفاده از روش‌های ناپارامتری هستیم که برای اجرای آن‌ها فرضیاتی در مورد توزیع داده‌ها وجود ندارد. به همین علت به روش‌های ناپارامتری گاهی «روش‌های توزیع-آزاد» (Distribution-free Methods) نیز می‌گویند.

داده‌های پارامتری به نمونه‌ای گفته می‌شود که از توزیع جامعه آماری آن مطلع هستیم. معمولا این توزیع آماری برای داده‌های کمی، نرمال یک یا چند متغییره در نظر گرفته می‌شود. در این حالت از آزمون‌های آماری پارامتری مثل آزمون T، آزمون F و یا آزمون Z استفاده می‌کنیم. همچنین برای اندازه‌گیری میزان همبستگی بین متغیرهای دو یا چند بعدی نیز از ضریب همبستگی پیرسون استفاده خواهیم کرد.

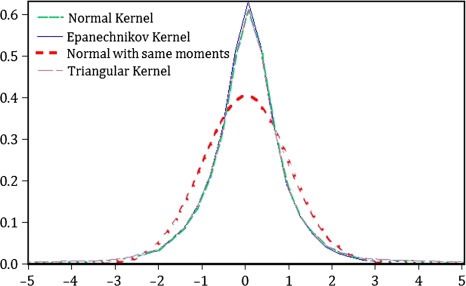
آمار پارامتریک به شاخه‌ای از آمار اطلاق می‌شود که با تجزیه و تحلیل داده‌ها بر اساس فرضیاتی در مورد توزیع اساسی داده‌ها سروکار دارد. در آمار پارامتریک فرض می‌شود که داده‌ها از یک توزیع احتمال خاص (مانند توزیع نرمال) پیروی می‌کنند و روش‌های تحلیل مورد استفاده بر این اساس انتخاب می‌شوند. این روش ها اغلب شامل تخمین پارامترهای توزیع فرضی مانند میانگین و واریانس هستند.

ویژگی های کلیدی آمار پارامتریک عبارتند از:

مفروضات: روش های پارامتریک بر فرضیات مربوط به توزیع داده ها تکیه دارند. مفروضات رایج عبارتند از نرمال بودن (داده ها از توزیع نرمال پیروی می کنند)، همگنی واریانس (واریانس ها در بین گروه ها برابر است) و استقلال مشاهدات.

پارامترها: روش های پارامتری شامل تخمین پارامترهایی است که توزیع مفروض را توصیف می کند. به عنوان مثال، در یک توزیع نرمال، میانگین و انحراف استاندارد پارامترها هستند.

آزمایش فرضیه: آمار پارامتریک اغلب شامل آزمون فرضیه است، که در آن داده‌های نمونه را با پارامترهای توزیع فرضی مقایسه می‌کنید. آزمون‌های رایج شامل آزمون‌های t، آنالیز واریانس (ANOVA) و تحلیل رگرسیون است.

قدرت آماری: زمانی که مفروضات برآورده می شوند، روش های پارامتری اغلب قوی تر از روش های ناپارامتریک هستند. این بدان معنی است که آنها در تشخیص اثرات واقعی یا تفاوت در داده ها بهتر هستند.

کارایی: روش‌های پارامتری معمولاً به نقاط داده کمتری برای دستیابی به سطح معنی‌داری آماری یکسان در مقایسه با روش‌های ناپارامتریک نیاز دارند.

دقت: روش‌های پارامتری می‌توانند تخمین‌های دقیق‌تری از پارامترهای جمعیت ارائه دهند که مفروضات برآورده شوند.

توزیع نرمال: بسیاری از روش های پارامتری فرض می کنند که داده ها از توزیع نرمال پیروی می کنند. با این حال، زمانی که داده ها این فرض را برآورده نمی کنند، نتایج ممکن است گمراه کننده باشند.

نمونه هایی از روش های آماری پارامتریک عبارتند از:

T-Tests: برای مقایسه میانگین ها بین دو گروه استفاده می شود.
آنالیز واریانس (ANOVA): برای مقایسه میانگین بین بیش از دو گروه استفاده می شود.
تحلیل رگرسیون: برای مدل‌سازی روابط بین متغیرها و پیش‌بینی استفاده می‌شود.
تجزیه و تحلیل بقای پارامتری: برای تجزیه و تحلیل داده های زمان تا رویداد، با فرض توزیع خاص برای زمان رویداد استفاده می شود.

توجه به این نکته مهم است که در حالی که روش های پارامتریک می توانند قدرتمند و کارآمد باشند، آنها به شدت بر این فرض تکیه می کنند که داده ها از توزیع خاصی پیروی می کنند. اگر این مفروضات نقض شوند، نتایج تجزیه و تحلیل ممکن است نادرست باشد. در مواردی که توزیع داده ها ناشناخته است یا به طور قابل توجهی از مفروضات انحراف دارد، روش های ناپارامتریک ممکن است مناسب تر باشند.

جهت دریافت پکیج های آموزشی آزمون های پارامتری در spss کلیک کنید .

اگر حجم نمونه در روش‌های تجزیه و تحلیل آمار پارامتری بزرگ انتخاب شود، معمولا توان آزمون مناسب خواهد بود و به راحتی می‌توان نتایج حاصل از آزمون فرض را به جامعه نسبت داد. جدول زیر به معرفی روش‌های پارامتری در انجام آزمون‌های فرض آماری پرداخته است.

مسئله	نوع آزمون	شرایط اجرای آزمون
مقایسه میانگین با مقدار ثابت از جامعه نرمال با واریانس معلوم	آزمون تک نمونه‌ای با آماره Z	مشاهدات بیشتر از 3۰ نمونه و چولگی نیز کم باشد.
مقایسه میانگین با مقدار ثابت از جامعه نرمال با واریانس نامعلوم	آزمون تک نمونه‌ای با آماره T	مشاهدات بیشتر از 20 نمونه و چولگی نیز کم باشد.
مقایسه میانگین دو جامعه مستقل نرمال با واریانس معلوم	آزمون دو نمونه‌ای با آماره Z	در هر گروه تعداد مشاهدات بیشتر از ۳۰ باشد و چولگی نیز کم باشد.
مقایسه میانگین دو جامعه مستقل نرمال با واریانس نامعلوم	آزمون دو نمونه‌ای با آماره z	در هر گروه تعداد مشاهدات بیشتر از 20 باشد و چولگی نیز کم باشد.
مقایسه میانگین زوجی	آزمون دو نمونه‌ای زوجی با آماره T	مشاهدات زوجی بیش از ۲۰ مشاهده باشند، چولگی نیز کم باشد.
مقایسه میانگین چند جامعه مستقل نرمال با واریانس برابر ولی نامعلوم	آنالیز واریانس (ANOVA)	تعداد مشاهدات نمونه در هر گروه از جامعه بیش از ۲۰ باشد. واریانس‌ها برابر یا تقریبا برابر باشند، هر جامعه دارای توزیع نرمال باشد.

آمار پارامتری و روش‌های تجزیه و تحلیل مرتبط