آزمون فرض آماری در spss – فرضیه h0 و h1
- 10 دی, 1400
- SPSS, روش تحقیق علوم رفتاری
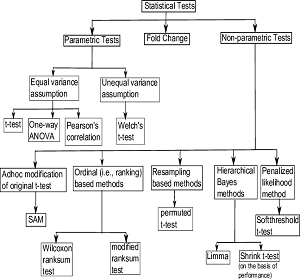
آزمون فرض آماری در spss
آزمون فرض آماری در spss
در این آموزش به آزمون فرض آماری در SPSS پرداخته ایم که شامل موارد زیر است :
مقدمه
فرض صفر و فرض مقابل
توزیع نمونه گیری آماره آزمون فرض یک طرفه و دو طرفه
مراحل کلی آزمون فرض آماری
ماهیت P-Value
آزمون آماری برای میانگین جامعه – آزمون t تک نمونه ای
آزمون آماری برای نسبت جامعه – آزمون دو جمله ای
آزمون اختلاف میانگین ها برای دو جامعه مستقل – آزمون t- دو نمونه مستقل
آزمون فرض آماری
تحقیقات همواره با سوال و فرضیه شروع می شوند. بسیاری از تحقیقات از مرحله سوال گذشته و به مرحله فرضیه می رسند. فرضیه حدس زیرکانه درباره پارامتر جامعه است. به فنون آماری مناسب برای تحلیل صحت یا نادرستی فرضیه ها فنون «آزمون فرض آماری» (Hypothesis testing) گفته می شود که در این فصل آنها را بررسی می کنیم.
به طور کلی هدف «آزمون فرض آماری» تعیین این موضوع است که با توجه به اطلاعات بدست آمده از داده های نمونه حدسی که درباره خصوصیتی از جامعه می زنیم به طور قوی تایید می شود یا نه. این حدس بنا به تحقیق نوعا شامل ادعایی درباره مقدار یک پارامتر جامعه است. «در واقع هر حکمی درباره جامعه را یک فرض آماری می نامند که قابل قبول بودن آن باید برمبنای اطلاعات حاصل از نمونه گیری از جامعه بررسی شود.»
چون ادعا ممکن است صحیح یا غلط باشد بنابراین دو فرض مکمل در ذهن بوجود می آید:
ادعا صحیح است فرض H0
ادعا غلط است فرض H1


با به کاربردن اطلاعاتی که از مشاهدات نمونه بدست می آید تصمیم گیرنده باید یکی از دو تصمیم یا استنباط را انتخاب کند:
فرض H1 را رد کند و نتیجه بگیرد که H0 بوسیله داده ها تایید می شود.
فرض H1 را رد نکند و نتیجه بگیرد که داده ها H0 را تایید نمی کند.
فرآِیند انتخاب یکی از دو تصمیم فوق را «آزمون فرض آماری» می نامند.
جهت دانلود پکیج های آموزشی و آموزش های ویدیویی در spss کلیک کنید .
قبول یا رد یک فرضیه آماری با اثبات و یا رد یک گزاره ریاضی متفاوت است.در ریاضی گزاره ای را اثبات و یا نفی می کنند و در هر حالت نتیجه اش که بدست می آید بدون هیچ شکی برقرار است ولی در مقابلنتیجه حاصل از «آزمون فرض آماری» به وسیله تحلیل داده های تجربی حتمی و قطعی نیست. شیوه مناسب برای آزمون فرض دارای مراحل منطقی است.
قبل از ذکر مراحل مورد نظر به بیان مفاهیم و اصطلاحات استفاده شده درآزمون پرداخته می شود. مهم ترین مرحله در «آزمون فرض آماری» تبدیل «فرضیه پژوهشی» و نقیض آن به «فرضیه های آماری» است. بنابراین مرحله فوق را با عنوان فرض صفر و فرض مقابل تشریح می کنیم.در این فصل به بیان برخی تعاریف در زمینه آمار استنباطی خواهیم پرداخت و سپس چهار آزمون آماری پرکاربرد در آمار کاربردی را معرفی خواهیم کرد.
فرض صفر و فرض مقابل
برای بحث درباره فرمول بندی مساله آزمون فرض آماری و حل آن به معرفی پاره ای از تعاریف و مفاهیم نیاز داریم.
مثال ۱:
نظریه ای پیشنهاد می کند که محصول یک واکنش شیمیایی معنی دارای توزیع نرمال (۱۶٫فرمول) X~N است.آزمایش گذشته نشان می دهد که اگر یک ماده معدنی به این محصول اضافه نشده باشد۱۰=µ و در غیر اینصورت۱۱=µ است. آزمایش ما عبارت است ازانتخاب نمونه تصادفی به حجم n .بر اساس این نمونه سعی خواهیم کرد تصمیم بگیریم کدام مورد درست است؟
پاسخ:
با توجه به فرضیه ای که در صورت مسئله بیان شده است دو فرض آماری زیر مطرح می شود:
میانگین جامعه برابر عدد ۱۰ است:۱۰=µ
میانگین جامعه برابر عدد۱۱است:۱۱=µ
در اینجا عدد نامعلوم برابر بودن ۱۱=µ است. از دو حکم فوق یکی را «فرض صفر»(Null Hypothesis) و دیگری را «فرض مقابل»(Alternative Hypothesis) می نامیم و آنهارا به ترتیب و به اختصاربا H0 و H1 نشان می دهیم برای اینکه معلوم شود کدام فرض را باید فرض صفر نامید لازم است که تفاوت اساسی بین دو اصطلاح فوق به روشنی درک شود. قبل ازاینکه ادعا کنیم حکمی معتبر است باید شواهد کافی در تایید آن بدست آوریم.
در نتیجه شخص تحلیلگر باید حمل را غلط بداند مگر اینکه داده های بدست آمده خلاف آنرا تایید کنند. به عبارت دیگر باید «فرض صفر» را صحیح دانست و فقط وقتی آنرا رد کرد که داده ها بر خلاف آن حکم کنند. تشابه زیادی بین این امر و محاکمه در دادگاه وجود دارد که در آن هیات منصفه فرض «مجرم بودن» را اتخاذ می کنند مگر اینکه شواهد قانع کننده ای مجرم بودن منتهی را ثابت کنند و نه اینکه در اثبات بی گناهی او بکوشند.
جهت مشاهده و دانلود فصل چهارم پایان نامه همراه با دیتا کلیک کنید .
با توجه به نکات فوق می توان نتیجه گرفت که هرگاه بخواهیم یک ادعا را از طریق تایید آن بوسیله اطلاعات حاصل از نمونه آزمون کنیم نفی آن ادعا را فرض صفر و خود آن رافرض مقابل می گیریم بنابراین فرض صفر و فرض مقابل در فرضیه فوق باید به این صورت باشد:
۱۰=µ:H0}
۱۱=µ:H1}
سطح معنی داری و خطاهای آماری
در ادامه آموزش آزمون فرض آماری در spss بعد از تعریف فرضیه های آماری قدم بعدی مشخص کردن درجه ای برای معنی دار بودن تفاوت ها (α) و حجمی برای نمونه مورد بررسی (n) است.روش این کار این است که فرض H0را به نفع فرض H1 رد می کنیم به شرط اینکه از یک آزمون آماری مقداری بدست آوریم که احتمال وقوع آن مقدار با توجه به H0 برابر با کمتر از یک احتمال بسیار کوچک باشد که با α نشان داده می شود.این احتمال وقوع کوچک را «سطح معنی داری» می گویند.
مقادیری که معمولا برای α استفاده می شود بیشتر از ۰٫۰۱ و۰٫۰۵ است. از آنجا که مقدار فرمول در تعیین اینکه H0 باید رد شود یا نه دخالت مستقیم دارد . الزام رعایت عینیت در تحقیق ایجاب می کند که α را پیش از شروع جمع آوری داده ها مشخص کنیم.
سطح معنی داری که محقق برای تعیین α در تحقیق انتخاب می کند براساس تخمین او از اهمیت و یا درجه قابلیت کاربرد یافته هایش مبتنی است. طبیعی است که اگر تحقیق مثلا درباره آثار درمانی عمل جراحی روی مغز باشد محقق باید α را خیلی کمتر در نظر بگیرد زیرا خطرهای رد کردن نادرست فرضیه صفر بسیار زیاد است.


هنگام اتخاذ تصمیم درباره H0 ممکن است دو نوع خطا پیش آید:
خطای نوع اول (Type I Error): رد کردن فرض H0 درحالی که درست است.
خطای نوع دوم (Type I Error): رد کردن فرض H0 درحالی که غلط است.
احتمال وقوع خطای نوع اول با α بزرگتر شود احتمال اینکه H0 را به غلط رد کنیم یا به عبارت دیگر احتمال اینکه مرتکب خطای نوع اول شویم افزایش می یابد. خطای نوع دوم معمولا با β نشان داده می شود α و β هم برای نشان دادن نوع خطاها و هم ارتکاب آن خطاها به کار می روند. یعنی:
( رد کردن H0 وقتی H0 درست است)P=(خطای نوع اول)P=α
(رد کردن H0 وقتی H1 درست است)P=(خطای نوع اول)P=β
احتمال α به مقدار مشخص پارامتر در دامنه ای بستگی دارد که H0 آنرا در بر می گیرد و حال آنکه β به مقدار پارامتر در دامنه ای بستگی دارد که H1 آنرا در بر می گیرد. این خطاها و احتمال آنها در رابطه با H0 را می توان بصورت زیر خلاصه کرد:
واضح است که بین α و β رابطه معکوس وجود دارد. بالا رفتن α و مقدار β کاهش می یابد و برعکس. این رابطه در آمار به «بده _ بستان» بین α و β معروف است. آنچه مسلم است مجموع α و β الزاما عدد یک نیست.واضح است که در هر استنباط آماری احتمال وقوع یکی از این دو نوع خطا وجود دارد و لازم است که آزمون کننده به نوعی سازش که تعادل بین احتمال وقوع این دو نوع خطا را به حد مطلوب برساند دست یابد.
جهت دانلود پکیج های آموزشی و آموزش های ویدیویی در spss کلیک کنید .
آزمونهای آماری مختلف احتمال تعادل های مختلفی را عرضه می کنند. در رسیدن به چنین تعادلی است که موضوع «توان آزمون» مطرح می شود. توان آزمون عبارت است از احتمال رد کردن H0 وقتی که H0 حقیقتا نادرست باشد. یعنی:
β – ۱ = (احتمال وقوع خطای نوع دوم) – ۱ = توان آزمون
آنچه موجب کاهش خطای نوع اول و دوم و همچنین توان آزمون می شود افزایش حجم نمونه است. منحنی های شکل ۱-۴ نشان می دهند که وقتی حجم نمونه (n) افزایش می یابد احتمال وقوع خطای نوع دوم (β) کاهش می یابد.
در این شکل افزایش توان آزمون دو طرفه میانگین وقتی که نمونه افزایش می یابد با یکدیگر مقایسه شده است. مشاهده می شود که وقتی حجم نمونه از ۴ به ۱۰٫۲۰٫۵۰و۱۰۰ افزایش می یابد چگونه توان آزمون زیادتر می شود.
توزیع نمونه گیری آماره
صحت یک فرضیه آماری فقط با استفاده از نمونه ای nتایی از جامعه آماری و توزیع نمونه گیری آماره مشخص میشود. در بحث «آزمون فرض» تایید یا رد «فرضیه صفر» به توزیع نمونه گیری آماره بستگی دارد. واضح است که توزیع آماره متاثر از توزیع جامعه و شرایط برآورد و همچنین حجم نمونه است. متغیرهای استاندارد مورد استفاده به کمک توزیع نمونه گیری تعریف می شوند. اصطلاح «آماره آزمون» یا پارامتر مورد آزمون تعریف می شود.
آزمون فرض یک طرفه و دو طرفه
براساس آنچه گفتیم نتیجه می گیریم که H0 را باید پذیرفت مگر آنکه دلیل محکمی بر رد آن وجود داشته باشد. این بدین معناست که فرض صفر همواره شامل سطح اطمینان ۱۰۰(α-۱) درصد است. بنابراین H1 در برگیرنده سطح معنی داری α است.
مفهوم کاربردی این جمله آن است که رد یا قبول H0 یا سطح اطمینان دلخواه صورت خواهد گرفت. پس همواره H1 به اندازه α در طرفین توزیع نمونه گیری تعریف خواهد شد. «یک طرفه» یا دو طرفه بودن آزمون فرض آماری به تعریف H0 و یا H1 بستگی دارد.
جهت مشاهده و دانلود فصل چهارم پایان نامه همراه با دیتا کلیک کنید .
مراحل کلی آزمون فرض آماری
از جمع بندی میانی آزمون فرض می توان برای همه آزمون فرض های آماری مراحل چهارگانه زیر را تدوین کرد. از این مراحل در طی فصول بعدی کتاب جهت تفسیر خروجی ها استفاده خواهد شد:
۱– تعریف فرضیه های آماری H0 و H1 فرض ها:
براساس قاعده ای که بیان شد چنانچه فرضیه پژوهشی یا هدف مرز مشخصی (-) داشته باشند H0 نشان دهنده ادعا خواهد بود در غیر این صورت نقیض آن در H0 قرار خواهد گرفت. آنچه مسلم است فرض H0 و H1 مکمل یکدیگرند. با این توصیف H0 گاهی بیان کننده ادعا و گاهی نقیض ادعا خواهد بود.
II– تعیین توزیع نمونه گیری آماره و نوع آماره آزمون (آماره آزمون):
توزیع نمونه گیری به شرایط تخمین پارامتر مورد ادعا بستگی دارد. بسته به اینکه فرضیه پژوهشی چه نوع پارامتری را بیان می کنند. توریع نمونه گیری آماره و آماره آزمون تغییر خواهد کرد.
III– تعیین سطح زیر منحنی H0 و H1 و محاسبه مقدار بحرانی (مقدار بحرانی):
سطح زیر منحنی H0 و H1 به توزیع نمونه گیری و مقدار α بستگی دارد. یک طرفه یا دو طرفه بودن آزمون نیز بر سطح زیر منحنی فرضیه های آماری تاثیر مستقیم دارد. چنانچه گفته شد: H0 در برگیرنده سطح اطمینان و H1 سطحی برابر α خواهد بود.
محاسبه مقدار استانداردی که تفکیک کننده H0 و H1 بصورت عددی باشد از دیگر موارد ضروری این مرحله است. مقدار استاندارد براساس نوع آزمون و مقدار α از جداول آماری موجود استخراج می شود. این مقدار با توجه به علامت آن «مقدار بحرانی» نامیده می شود. مقدار استاندارد وجدول آماری مورد نیاز برای استخراج آن براساس آماره آزمون تعیین می شود. برای مثال اگر آماره آزمون از نوع Z باشد مقدار بحرانی براساس جدول استاندارد Z تعیین می شود و اگر از نوع F باشد براساس جدول F تعریف می شود.
IV . تصمیم گیری:
در این مرحله مقدار آماره آزمون محاسبه شده در مرحله دوم یا مقدار بحرانی مرحله سوم مقایسه می شود. چنانچه آماره آزمون در ناحیه پذیرش H0 قرار گیرد. گفته می شود که رد سطح اطمینان مورد نظر دلیل کافی برای پذیرش H0 وجود دارد. در غیر اینصورت فرض H0 رد شده و H1 آیا در سطح خطای α درصد پذیرفته می شود.
پس از تایید یا رد H0 تحلیلگر باید بطور مشخص بیان کند که آیا فرضیه پژوهشی پذیرفته یا رد شده است. بدیهی است محقق هیچگاه ادعای اثبات یا عدم اثبات فرضیه پژوهشی یا فرضیه های آماری را ندارند بلکه در تحلیل خود به لحاظ استقرار احتیاط را رعایت کند.
ماهیت P-Value
P-Value یک آزمون آماری مقدار احتمالی است که میزان سازگاری داده های نمونه را با نتیجه H0 اندازه می گیرد. این مقدار خلاصه ای فشرده از یافته های نمونه ای را در یک آزمون آماری معرفی می کند و غالبا در گزارشهای منتشر شده نتایج آزمون آماری و در خروجی برنامه ها کامپیوتری مورد استفاده واقع می شود.
برای یک آزمون یک طرفه مربوط به میانگین جامعه P-Value برحسب آماره آزمون استاندارد شده *Ζ بصورت زیر تعریف می شود:
P-Value یک آزمون آماری یک طرفه برای µ عبارت است از احتمال آنکه اگر µ۰ = µ آماره آزمون استاندارد شده *Z در جهت ناحیه رد می تواند کمتر از مقداری باشد که واقعا مشاهده شده است.
آزمون P-Value
در ادامه یادگیری آزمون فرض آماری در spss همانطورکه قبلا گفتیم P-Value یک آزمون برای µ میزان سازگاری بین بر آمد نمونه ای و مقدار µ۰ را که در H0 مسلم فرض شده است اندازه می گیرد. یک P-Value بزرگ نشان می دهد که µ۰ موجه است و بنابراین باید H0 نتیجه گرفته شود.
در واقع برحسب اینکه P-Value بزرگتر یا کوچکتر از α (ناحیه بحرانی) باشد که از آزمون مبتنی بر P-Value بدست می آید از نظر ریاضی هم ارز یا نتیجه ای است که از قاعده تصمیم متناظر مبتنی بر آماره آزمون استاندارد شده حاصل می شود. قاعده تصمیم مبتنی بر P-Value بصورت زیر است:
اگر P-Value ≥ α باشد گزینه H0 را نتیجه بگیرید.
اگر P-Value ≤α باشد گزینه H1 را نتیجه بگیرید.
با استفاده از یک P-Value یک طرفه یا دو طرفه هر کدام که مقتضی باشد این قاعده تصمیم خواه آزمون یک طرفه یا دو طرفه باشد صادق است.
۴-۸ آزمون آماری برای میانگین جامعه – آزمون t تک نمونه ای
وقتی می خواهیم برای میانگین جامعه (µ) آزمونی انجام دهیم. در واقع علاقه مندیم آزمون کنیم که آیا میانگین جامعه برابر عدد مشخصی هست یا خیر؟ در این حالت فرض های آماری عبارتند از:
µ=µ۰ : H0
H1 : µ≠µ۰
از آنجایی که در عمل همواره واریانس جامعه نامعلوم است آزمون مناسب آزمون t تک نمونه ای می باشد.
مثال ۱) داده های زیر نمره های ۲۰ دانش آموز در درس آمار است:
۱۷٫۵٫ ۱۴٫ ۱۳٫۵٫ ۱۶ .۱۴٫۵٫ ۲۰ . ۱۳ . ۱۲٫ ۱۶٫۵٫ ۱۹٫ ۱۶٫ ۱۰٫۵ . ۱۷٫ ۱۲٫ ۱۳٫ ۱۴٫۵٫ ۱۷٫ ۱۱٫ ۱۹٫۸٫ ۱۲٫۵
آیا میتوان گفت میانگین نمره های دانش آموزان این کلاس برابر ۱۵ است؟
در واقع می خواهیم آزمون فرض زیر را انجام دهیم:
µ=۱۵ : H0
H1 : µ≠۱۵
برای انجام ای آزمون مسیر Analyze>Compare Means>One-Sample T Test را طی کنید تا کادر مکالمه ای One-SampleT Test باز شود. در این کادر متغیر “نمره” را در جعبه Test Variable و درجعبه Test Values عدد ۱۵ را تایپ کنید.
جهت دانلود پکیج های آموزشی و آموزش های ویدیویی در spss کلیک کنید .
آزمون فرض آماری در spss
سپس گزینه OK را بزنید تا خروجی آزمون را ببینید.
معرفی جداول: جدول اول (One-Sample Statistics) حجم نمونه شاخص های آماری میانگین . انحراف معیار و خطای معیار میانگین را نشان می دهد. جدول دوم (One-Sample Test) نتایج آزمون t تک نمونه ای را نشان می دهد. مقدار آماره t محاسبه شده برابر با ۰/۰۷۹ – شده است که می دانیم آماره مربوط به آن به صورت زیر است و دارا توزیع t یا n-1 درجه آزادی (df) است.
عبارت sig که مخفف significant levele و به معنی “سطح معنی داری” است نشان دهنده P مقدار آزمون است که در این آزمون برابر ۰/۹۴ شده است. همچنین مقدار Mean Difference نشان دهنده Χ-µ۰ است که در اینجا برابر است با ۰/۰۵-=۱۴/۹۵-۱۵
در قسمت بعد ۹۵%Confidence Interval فاصله اطمینان ۹۵ % را برای پارامتر Χ-µ۰ نشان می دهد که در این مثال برابر (-۱/۳۷ _۱/۲۷) است حال اگر بخواهیم فاصله اطمینان برای فرمول بدست آوریم باید نا معادله فرمول را برای مجهول Χ-µ بین دو عدد ۱٫۳۷- و ۱٫۲۷ حل کنیم لذا فاصله اطمینان برای فرمول برابر است با( ۱۳/۶۸ _۱۶/۳۲).
۳- روش فاصله اطمینان: در اینجا فرضیه ۰=۱۵-µ :H0 که معادل است با ۱۵=µ :H0 را بررسی می کنیم. بنابراین برای آزمون فرضیه فوق به روش فاصله اطمینان کافیست که چک کنیم آیا فاصله اطمینان۱۵-µ عدد صفر را شامل می شود؟ در صورتی که فاصله اطمینان شامل عدد صفر باشد تصمیم به عدم رد فرض H0 خواهیم گرفت و با توجه به فاصله اطمینان ۹۵ % در این مثال در سطح معنی داری۰/۰۵ فرض H0 یعنی فرض برابری را رد نمی کنیم.
مثال ۲) در مثال ۱ فرضیه ۱۲=فرمول : H0 را آزمون کنید.
در این حالت همه مراحل بیان شده در مثال قبل را انجام خواهیم داد با این تفاوت که عدد ۱۲ را در جعبه Test Values تایپ می کنیم و خروجی زیر را خواهیم دید
از سه روش میتوان نشان داد که فرضیه ۱۲= فرمول :H0 در سطح معنی داری۰/۰۵ رد می شود(؟).
توجه:
از آنجایی که در عمل هیچگاه واریانس جامعه معلوم نیست در SPSS نیز آزمون از طریق آماره Z تعبیه نشده است.
در این آزمون فرض بر این است داده ها از جامعه ای با توزیع نرمال هستند.
در SPSS گزینه انجام آزمون های یک طرفه تعبیه نشده است. اما در آزمون هایی که آماره آنها از توزیع t که توزیعی متقارن است پیروی می کند. P- مقدار آزمون یک طرفه نصف P- مقدار آزمون دو طرفه است (؟). لذا در این آزمون نیز می توان آزمون های یک طرفه را انجام داد.
آزمون آماری برای نسبت جامعه – آزمون دو جمله ای
مثال ۳) فرض کنید سکه ای را ۳۰ مرتبه پرتاب کرده اید و نتایج به صورت زیر بدست آمده است(۱-شیر.۰-خط)
۰٫۰٫۰٫۰٫۰٫۰٫۰٫۰٫۰٫۰٫۰٫۰٫۰٫۰٫۰٫۰٫۰٫۰٫۱٫۱٫۱٫۱٫۱٫۱٫۱٫۱٫۱٫۱٫۱٫۱
می خواهیم آزمون کنیم که آیا سکه سالم است یا خیر؟ می خواهیم فرض های زیر را آزمون کنیم:
H0 = p = 0.5
H1 = p ≠ ۰٫۵
برای آزمون این فرض از آزمون دو جمله ای استفاده می کنیم.
برای انجام این کار داده های بالا را به عنوان متغیر Toss وارد کرده و مسیرAnalyze>Nonparametric Tests>Legacy Diolog>Binomial را طی کنید تا کادر مکالمه ای Binomial Test باز شود.
آزمون فرض آماری در spss
متغیر Toss را به قسمت Test Variable List وارد کرده و مقدار Test Proportion را ۰٫۵ وارد کنید و در قسمت Define Dichotomy گزینه Get from data را انتخاب کنید و سپس دکمه OK را کلیک کنید تا خروجی زیر ظاهر شود:
معرفی جداول: در ستون اول دو گروه جامعه را نشان می دهد و در ستون دوم آنها را معرفی می کند. توجه داشته باشید که در SPSS هر گروهی که کدش اول وارد شود را به نام گروه اول (اصلی) می شناسد و نسبت P برای این گروه تعریف می شود.
برای مثال اگر اولین عدد در وارد کردن داده های مربوط به متغیر Toss را “۱” وارد کنیم عدد “۱” را به عنوان کد گروه اول می شناسد و نسبت P را برای این گروه (شیر بودن) و نسبت ۱-P را برای گروه دیگر (خط بودن) در نظر می گیرد.
در ستون سوم N تعداد افراد مشاهده شده در هر گروه را نشان می دهد و در ستون بعد نسبت مشاهده شده هر گروه را نشان می دهد. در ستون پنجم Test Prop. عدد مورد آزمون در فرض صفر را نشان می دهد که در اینجا۰٫۰۵ است. در ستون آخر (P ,Exact Sig.(2-tailed-مقدار دقیق را در حالت دو طرفه نشان می دهد.
تفسیر: با توجه به اینکهP-مقدار دقیق دو طرفه بیشتر از ۰٫۰۵ است فرض صفر سالم بودن سکه را رد نمی کنیم.
در یک نمونه ی تصادفی ۱۰۰۰۰ نفری از جامعه ی بزرگ تعداد ۱۰۰ مورد از یک بیماری خاص مشاهده شده در سطح اطمینان ۹۵ درصد آزمون کنید که:
الف) آیا نسبت مبتلایان به بیماری خاص در جامعه از ۰٫۰۲ کم تر است؟
ب) آیا می توان گفت نسبت مبتلایان به بیماری خاص در جامعه برابر ۰٫۰۲ است یا خیر؟
– این داده ها را با استفاده از دستور weighte cases وارد کنید.
الف)تمام مراحل مربوط به مثال ۱ را در اینجا انجام می دهیم با این تفاوت که در قسمت Test Proportion از کادر مکالمه ایBinomial Test عدد ۰٫۰۲ را جایگزین عدد ۰٫۵ می کنیم و سپس دکمه OK را میزنیم و خروجی را به صورت زیر خواهیم داشت.
توجه داشته باشید که اگر مقدار Test Proportion از ۰٫۵ کمتر باشد آزمون به صورت یک طرفه انجام می شود و فرض H0 به صورت P < 0.02 خواهد بود لذا با توجه به اینکه –P مقدار از ۰٫۰۵ کمتر است فرض صفر را رد نمی کنیم.
ب) به علت وجود تقارن توزیع نرمال و این که در این حالت SPSS آزمون دو طرفه را انجام نمی دهد. برای انجام آزمون دو طرفه P-مقدار آزمون یک طرفه را دو برابر می کنیم در این حالت باز هم میبینیم کهP-مقدار از ۰٫۰۵ کمتر است بنابراین فرض صفر را رد نمی کنیم.
توجه:
آزمونهایی که در بالا انجام شده از طریق توزیع نرمال استاندارد است. اما می دانیم که صورت مساله برای یک توزیع گسسته (دو جمله ای) مطرح شده بود. لذا نتایج آزمونهای فوق همواره بصورت مجانبی (تقریبی) بوده و برای نمونه ای بزرگ صحیح است.
اگر بخواهیم آزمون را در نمونه ای کوچک انجام دهیم بهتر است از روشهای شبیه سازی مونت کارلو استفاده کنیم برای این کار می توانیم از گزینه Exact در کادر مکالمه ای Binomial Test استفاده کنیم و گزینه Monte Carlo را تیک زده و سپس دکمه های Continue و Ok را بزنیم.
جهت دانلود پکیج های آموزشی و آموزش های ویدیویی در spss کلیک کنید .
آزمون فرض آماری در spss
آزمون اختلاف میانگین ها برای دو جامعه مستقل – آزمون t- دو نمونه مستقل
این آزمون زمانی به کار می رود که بخواهیم میانگین یک متغیر کمی را در بین دو گروه مستقل باهم مقایسه کنیم. برای مثال مقایسه فشارخون دو گروه افراد بعد از استفاده از داروهای A و B .
در آزمون t-دو نمونه مستقل فرضیات زیر را مورد بررسی قرار می دهیم:
۰=H0 : µ۲- µ۱
۰≠H1 : µ۲- µ۱
برای استفاده صحیح از این آزمون نیاز به اطلاع در مورد برابری و یا نابرابری واریانس های دو گروه خواهیم داشت. لذا ابتدا بایستی با استفاده از آزمون Levene برابری واریانس های دو گروه را مورد بررسی قرار داد.دو حالت می تواند پیش آید که هر دو حالت در SPSS به طور همزمان اجرا می شود.
برابری واریانس ها: چنانچهP-مقدار حاصل از آزمون Levene بیشتر از α باشد می توان نتیجه گرفت که واریانس های دو گروه باهم برابر است. در این حالت برای بررسی معنی داری اختلاف بین میانگین های دو گروه از آزمون “t- دو نمونه مستقل در حالت برابری واریانس ها” استفاده می کنیم.
نابرابری واریانس ها: چنانچهP-مقدار حاصل از آزمون Levene کمتر مساوی α باشد می توان نتیجه گرفت که واریانس های دو گروه باهم برابر نیستند. در این حالت برای بررسی معنی داری اختلاف بین میانگین های دو گروه از آزمون “t- دو نمونه مستقل در حالت نابرابری واریانس ها” استفاده می کنیم.
مثال ۵) ده دانش آموز پسر و ده دانش آموز دختر به دلخواه انتخاب شده اند و وزن آنها اندازه گیری شده است. داده ها بصورت زیرند:
دختر
۵۵ ۶۳ ۶۰ ۴۵ ۵۷ ۴۵ ۶۰ ۶۵ ۴۸ ۵۴
پسر
۷۵ ۹۰ ۸۵ ۷۰ ۶۸ ۷۲ ۷۴ ۸۰ ۶۸ ۷۵
مایلیم بدانیم آیا وزن دانش آموزان دختر و پسر از لحاظ آماری باهم برابر است؟
ابتدا داده ها را به صورت زیر در SPSS وارد کنید.مردان با کد ۱ و زنان با کد ۲ مشخص شده اند.
برای انجام این آزمون مسیر Analyze>Compare Means>Independent-Samples T Test را طی کنید. تا کادر مکالمه ای Independent-Samples T Test باز شود. در این کادر متغیر “Weight” را در جعبه Test Variable(s) و متغیر “Sex” را در جعبه Grouping Variable وارد کنید. روی دکمه Define Groups کلیک کنید و سپس Ok را کلیک کنید تا خروجی به صورت زیر ظاهر شود:
معرفی جدول: این جدول شامل ۳ قسمت است:
Group Statistics : شامل تعداد نمونه و شاخص های آماری به تفکیک هر یک از گروه هاست.
Levene’s Test : شامل آزمون Levene برای آزمون برابری واریانس ها(آماره F وP-مقدار)
t-test for Equality of Means : نتایج آزمون t-دو نمونه ای مستقل است که ستون های آن به ترتیب از چپ به راست عبارتند از:مقدار آماره t.
درجه آزادی P-مقدار آزمون دوطرفه sig(two-) (tailed). اختلاف میانگین ها .(Difference Mean) خطای استاندارد اختلاف میانگین ها (Std. Error Difference )و فاصله اطمینان ۹۵ % برای (۹۵% Confidence Interval of the Difference). همه این نتایج برای دو حالت بیان شده اند. مقادیر خط اول برای حالت برابری واریانس ها و مقادیر خط دوم برای حالت نابرابری واریانس ها هستند.
تفسیر:P- مقدار آزمون Levene نشان می دهد که بین واریانس وزن دانش آموزان پسر و دختر اختلاف معنی داری وجود ندارد لذا باید نتایج ازمون t را از خط دوم قسمت مربوطه گزارش کرد در اینجا نیز می توانیم از سه روش ناحیه رد. P-مقدار. فاصله اطمینان آزمون فرض را انجام دهیم.
روش p- مقدار: در این مثال P-مقدار ۰٫۰۰۰ گزارش شده است و لذا کمتر از ۰٫۰۵ است بنابراین در سطح معنی داری ۰٫۰۵ فرض H0 یعنی فرض برابری را قبول نمی کنیم و معنی داری اختلاف را می پذیریم.
روش فاصله اطمینان: در اینجا فرضیه ۰ = H0 : µ۱-µ۲ بررسی می کنیم بنابراین برای آزمون فرضیه فوق به روش فاصله اطمینان کافیست که چک کنیم آیا فاصله اطمینان عدد صفر را شامل می شود؟ با توجه به فاصله اطمینان ۹۵ % در این مثال در سطح معنی داری ۰٫۰۵ فرض H0 یعنی فرض برابری را قبول نمی کنیم و معنی داری اختلاف را می پذیریم.
جهت دانلود پکیج های آموزشی و آموزش های ویدیویی در spss کلیک کنید .
جهت مشاهده و دانلود فصل چهارم پایان نامه همراه با دیتا کلیک کنید .
جهت مشاهده جدید ترین آموزش های ویدویی در spss کلیک کنید .
جهت دانلود فصل چهارم پایان نامه همراه با دیتا در چهار نرم افزار Pls , Lisrel , Amos , Spss کلیک کنید .
جهت دانلود پروژه و دیتا همراه با تحلیل در spss کلیک کنید .
جهت دانلود آموزش های رایگان spss کلیلک کنید
روش تحقیق در علوم رفتاری
آزمون فرض آماری در spss