شاخص های آماری

مرحله اول آمار توصيفي يعني تشكيل جداول فراواني و رسم نمودارهاي آماري در SPSS بيان شد. مرحله دوم در آمار توصيفي،خلاصه كردن داده ها در قالب اعدادي است كه موسوم به شاخصهاي آماري هستند.
شاخص های آماری به دو دسته تقسيم ميشوند: شاخصهائي كه گرايش به مركز يا مركزيت داده ها را اندازه ميگيرد(شاخص های مركزی) و شاخصهائي كه براي اندازه گيري تغيير پذيري داده ها به كار ميرود(شاخص های پراكندگی).

یک شاخص آماری نمایش داده های آماری برای زمان، مکان یا هر مشخصه مرتبط دیگر است که حداقل برای یک بعد (معمولاً اندازه) تصحیح می شود تا امکان مقایسه های معنادار را فراهم کند.

این مقیاس خلاصه ای است که به یک موضوع یا پدیده کلیدی مربوط می شود و از یک سری واقعیت های مشاهده شده ناشی می شود. از شاخص ها می توان برای آشکار کردن موقعیت های نسبی یا نشان دادن تغییرات مثبت یا منفی استفاده کرد. شاخص ها معمولا ورودی مستقیمی به سیاست های کلیه کشور ها هستند. در زمینه های سیاست استراتژیک، شاخص های آماری برای تعیین اهداف و نظارت بر دستیابی به آنها مهم هستند.

به خودی خود، شاخص ها لزوماً همه جنبه های توسعه یا تغییر را شامل نمی شوند، اما به شدت به توضیح آنها کمک می کنند. آنها امکان مقایسه در طول زمان را بین، به عنوان مثال، کشورها و مناطق فراهم می کنند و از این طریق به جمع آوری “شواهد” برای تصمیم گیری کمک می کنند.

شاخص‌های آماری معیارها یا معیارهایی هستند که برای خلاصه کردن و توصیف جنبه‌های مختلف داده‌ها یا پدیده‌ها استفاده می‌شوند. آنها بینش های ارزشمندی را ارائه می دهند و به محققان، تحلیلگران، سیاست گذاران و تصمیم گیرندگان کمک می کنند تا الگوها، روندها، روابط و ویژگی های درون مجموعه داده ها را درک کنند. شاخص های آماری به عنوان ابزاری برای تجزیه و تحلیل کمی، تسهیل مقایسه، ارزیابی و تصمیم گیری آگاهانه عمل می کنند. در اینجا برخی از انواع رایج شاخص های آماری آورده شده است:

شاخص های مرکزی گرایش:
میانگین (متوسط): مجموع همه مقادیر تقسیم بر تعداد کل مقادیر. این یک اندازه گیری از مقدار “معمولی” در یک مجموعه داده را ارائه می دهد.
میانه: مقدار وسط وقتی که همه مقادیر به ترتیب مرتب شده باشند. نسبت به میانگین حساسیت کمتری نسبت به نقاط پرت دارد.
حالت: متداول ترین مقدار در یک مجموعه داده است.

شاخص های متغیر و پراکندگی:
محدوده: تفاوت بین مقادیر حداکثر و حداقل در یک مجموعه داده.
واریانس: اندازه گیری میزان پراکندگی مقادیر از میانگین.
انحراف استاندارد: جذر واریانس که معیاری از میانگین انحراف از میانگین را ارائه می دهد.

شاخص های شکل توزیع:
چولگی: عدم تقارن توزیع مقادیر حول میانگین را اندازه می گیرد.
کورتوزیس: “دمی بودن” یا اوج بودن یک توزیع را در مقایسه با توزیع نرمال اندازه گیری می کند.

درصد و ربع:
درصدها: مقادیری که یک مجموعه داده را به نسبت های خاصی تقسیم می کند. میانه صدک 50 است.
ربع: مقادیری که یک مجموعه داده را به چهار قسمت مساوی تقسیم می کند. چارک اول (Q1) صدک 25، چارک دوم (Q2) میانه و چارک سوم (Q3) صدک 75 است.

شاخص های همبستگی و رابطه:
ضریب همبستگی: قدرت و جهت یک رابطه خطی بین دو متغیر را اندازه گیری می کند.
کوواریانس: چگونگی تغییر دو متغیر را با هم اندازه گیری می کند.

شاخص های احتمال و ریسک:
احتمال: احتمال وقوع یک رویداد.
معیارهای ریسک: شاخص‌هایی مانند انحراف استاندارد، ارزش در معرض خطر (VaR) و ارزش شرطی در معرض خطر (CVaR) که در امور مالی برای تعیین کمیت زیان‌های احتمالی استفاده می‌شوند.

اعداد فهرست:
شاخص قیمت مصرف کننده (CPI): تغییرات سطح متوسط قیمت سبدی از کالاها و خدمات را در طول زمان اندازه گیری می کند.
شاخص جینی: نابرابری درآمد را در یک جمعیت اندازه گیری می کند.

شاخص های کیفیت مناسب و مدل:
ریشه میانگین مربعات خطا (RMSE): میانگین انحراف بین مقادیر پیش بینی شده و واقعی را در یک مدل رگرسیونی یا پیش بینی اندازه گیری می کند.
تست‌های خوبی برازش: شاخص‌هایی مانند آزمون مجذور کای برای ارزیابی میزان تناسب یک توزیع مشاهده‌شده با توزیع مورد انتظار استفاده می‌شوند.

نشانگرهای اقتصادی:
تولید ناخالص داخلی (GDP): تولید اقتصادی یک کشور را اندازه گیری می کند.
نرخ بیکاری: نسبت نیروی کار بیکار را اندازه گیری می کند.

این شاخص‌ها تنها گزیده‌ای از بسیاری از ابزارهای موجود برای خلاصه‌سازی و تفسیر داده‌ها هستند. انتخاب شاخص ها به نوع داده ها، سوال تحقیق و زمینه خاصی که تحلیل در آن انجام می شود بستگی دارد.

در علم آمار دو نوع شاخص وجود دارد : شاخص های مرکزی، شاخص های پراکندگی که هر کدام از این ها زیر مجموعه ای دارند که در ادامه به بررسی آن ها میپردازیم.

شاخص های مركزی:

شاخصهاي مركزي مهم عبارتند از:
مد Mode :مد داده اي است كه بيشترين فراواني را دارد.استفاده از اين شاخص بيشتر در متغيرهاي رسته اي است

ميانه Median و چندكها: ميانه به داده وسطي داده ها اطلاق ميشود و در داده هاي كم تعداد يك شاخص پركاربرد و كار آمد است.
ميانه داده اي است كه تقريباً نصف داده ها از آن كمتر و نصف داده ها از آن بيشترند.
تعريف چندكها هم معادل ميانه است،چندك مرتبه، pمقداري است كه تقريباً 100pدرصد داده ها از آن كمتريا مساوي آن و 100(1-p) درصد داده ها از آن بيشرند. ساده ترين نوع چندكها ، چاركها Quartiles و دهكها هستند.
– چارك اول: مقداري است كه يك چهارم داده ها از آن كمتر يا مساوي با آن هستند.
– چارك دوم: معادل ميانه است.
– چارك سوم: مقداري است كه سه چهارم داده ها از آن كمتر يا مساوي با آن هستند.
– دهك اول: مقداري است كه يك دهم داده ها از آن كمتر يا مساوي با آن هستند. ساير دهكها هم بـه همـين صورت تعريف مي شوند.

ميانگين Mean: پركاربردترين و كاراترين شاخص براي اندازه گيري مركزيت داده ها ميانگين است. البته در صورتيكه تعداد داده ها كم باشد يا تعدادي داده پرت در ميان داده هامشاهده شود، دقت ميانگين كاهش خواهد يافت لذا درصورتيكه يكي از حالات فوق اتفاق بيفتد بايد در استفاده از ميانگين هوشيار بود.
براي رفع مشكل داده هاي پرت، انواع ديگري از ميانگين تعريف ميشود كه اثر اينگونه داده ها را كاهش ميدهد.

شاخص های پراكندگی:

غير از شاخصهائي كه گرايش داده ها را به يك مقدار مركزي نشان ميدهد، علاقه مند به شاخصهائي هستيم كه به نوعي ميزان پراكندگي داده ها را بيان كنند. مهمترين شاخصهاي آماري پراكندگي عبارتند از:
دامنه تغييرات Range: تفاضل بزرگترين و كوچكترين داده را دامنه تغييرات مي نامند.
واريانس Variance: ميانگين مربعات تفاضل داده ها از ميانگين را واريانس گويند.

انحراف معيار Standard division: جذر واريانس را انحراف معيار گويند.
انحراف استاندارد ميانگين Standard Error of Mean: جذر حاصل تقسيم واريانس بر تعداد داده ها را انحراف استاندارد ميانگين گويند.
براي محاسبه شاخصهاي بالا، ابتدا مسير زير را طي كنيد:

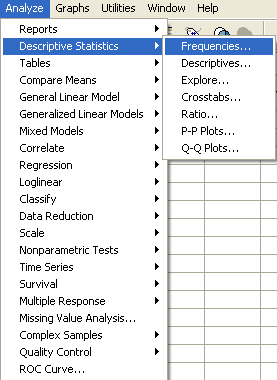
روي دكمه statistics كليك كنيد.كادر زير باز خواهد شد. شاخصهاي مركزي را ميتوانيد از كادر Central Tendencyو شاخصهاي پراكندگي را از كادر Dispersionانتخاب كنيد.
پس از انتخاب شاخصهاي مورد نظر دكمه Continueو سپس OKرا كليك كنيد

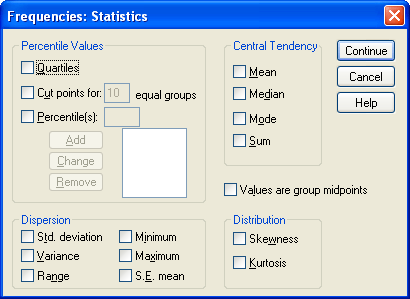
و يا ميتوان از مسير زير استفاده كرد:

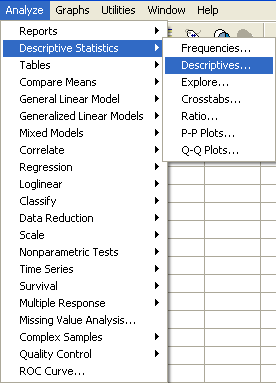
روي دكمه … Optionكليك كنيد و شاخصهاي موردنظرتان را انتخاب كنيد:

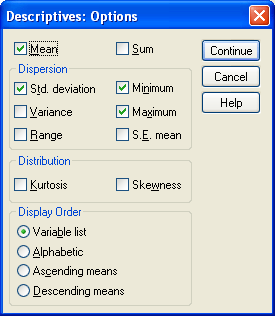
در قسمت بعدی آموزش به بحث box plot میپردازیم.

شاخص های آماری